O pedido
Para você que tá sem idéias, puxe uma cadeira e escute essa daqui...

Em uma noite de sábado, 18 de junho de 2022, pedi minha namorada em casamento dentro do seu jogo favorito. Ainda chocada, me laçou o pescoço com os braços e falou o "sim" com o sorriso mais sincero. Neste momento consolidei na nossa memória um momento íntimo e inesquecível. Desde então, sempre que nos lembramos deste instante a gente se diverte.
Hoje, dois anos depois, muito felizes e muito bem casados, temos uma filhinha de dois meses dormindo no quarto ao lado. Isso meu amigo, que eu considero como sucesso.
Mas e você? Sente que está pronto para dar os próximos passos como eu dei?
Há quem não sabe nem por onde começar. Há quem não se considera criativo o suficiente. Para todos os casos, eu nutro uma convicção que este texto te inspirará. Contarei bem mais do porquê desse pedido ter dado certo. Humildemente, peço que confie e mim pelos próximos minutos e navegue pelas reflexões que vou trazer pra ti.
Vamos lá?
Prefácio
Rotina desafiadora
A ambição profissional deste casal o levou à uma rotina desafiadora em 2022. Morávamos em São Paulo capital e ambos quase abrimos mão do homeoffice para trabalhar presencialmente no Rio de Janeiro em melhores oportunidades profissionais.
Digo "quase abrimos mão" porque minhas viagens aconteciam em semanas alternadas. Já a minha esposa, que era líder de uma operação de vendas em regime presencial. Toda segunda-feira enfrentava os mesmos 38' para o aeroporto à caminho da cidade maravilhosa. Na atividade dela a presença é fundamental, principalmente em final de mês quando é época de fechamento de metas de vendas.
Por um ano vivemos a mesma agenda: quando não estávamos viajando juntos à trabalho, passávamos a semana inteira apartados na espera pelo fim de semana. Logo, você consegue imaginar a correria de desfaz-malas-e-refaz-malas recorrente. Nossa manutenção do relacionamento acabava por as vezes competir com todas as atividades domésticas e qualquer outro evento social de família e amigos.
Em algum momento após vários meses nesse cenário exaustivo, aproveitamos um feriado para viajar à minha cidade natal em Minas. De maneira bem despretenciosa, meu irmão compartilhou conosco um joguinho chamado Termo. Confesso nunca ter ouvido falar até então. Mal sabíamos que se tornaria uma uma rotina inegociável na vida dos Bibos, que é como nós nos chamamos de forma carinhosa.
Termo & Wordle
O jogo foi desenvolvido em 2022 pelo Fernando Serboncini (acompanha ele no X aqui) que, por sua vez, é um copycat turbinado de outro jogo chamado Wordle: um jogo de adivinhar palavras que simula a mesma lógica do jogo antigo Senha, trocando as cores por letras.
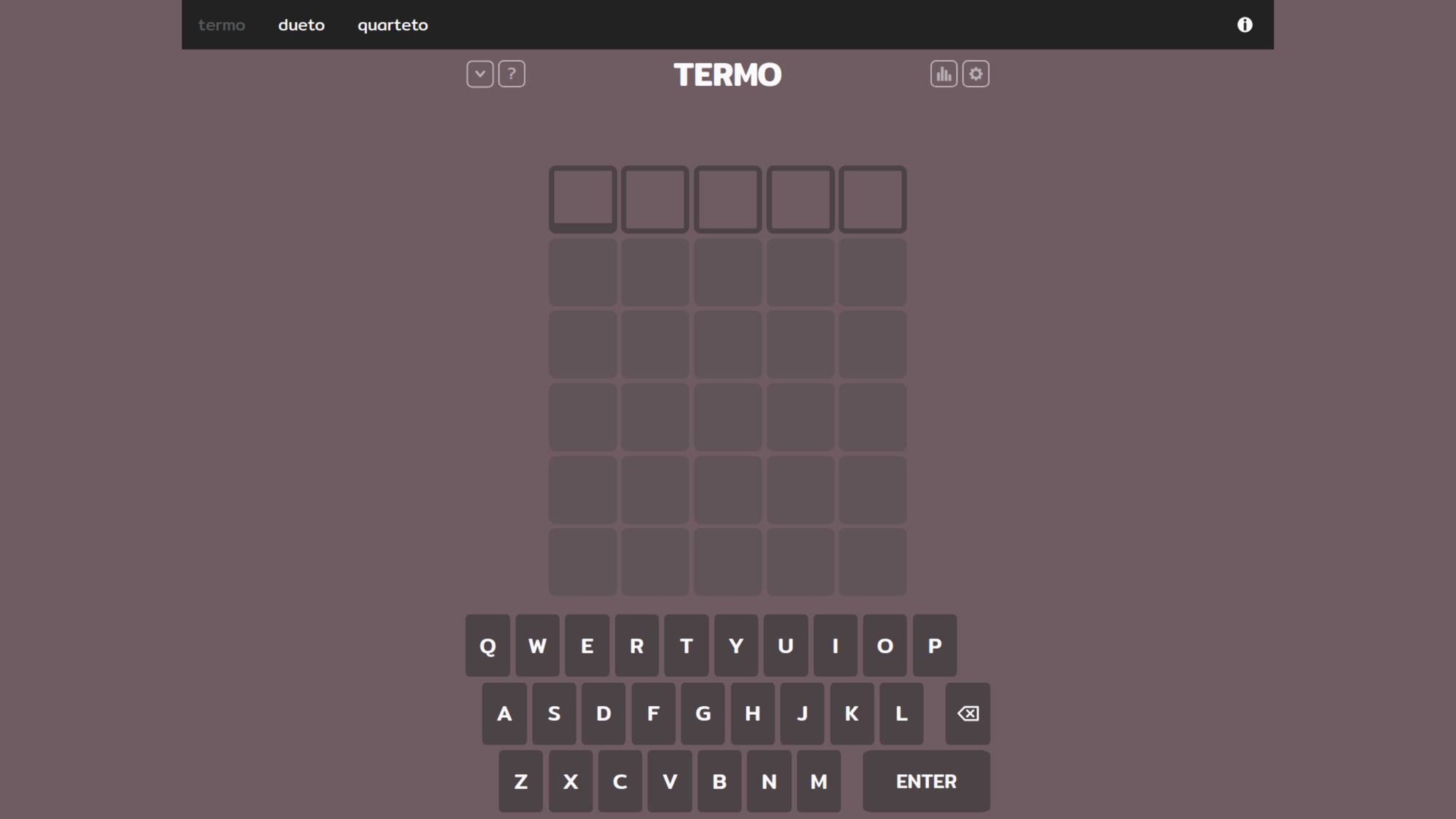
Termo, jogo do Fernando Serboncini
A versão original desenvolvida em 2021 pelo Josh Wardle tem uma história carinhosa. Sua companheira Palak Shah adorava palavras cruzadas e todo qualquer jogo de palavras. Naquele ano de pandemia, aproveitou para propor uma nova rotina de 3min diários para descobrir a palavra "por dia". Tem toda a história neste artigo do NY Times, recomendo a leitura.
Wordle interface
Em algum momento depois, Josh e Palak decidiram compartilhar o jogo com amigos. O Wordle ganhou vida própria e em meses atingiu milhões de usuários. O jogo fez tanto sucesso que no fim do ano seguinte Josh vendeu o Wordle para o New York Times.
Nota: Engraçado que mal sabe o Fernando o tanto que ele impactou nossa vida. O sucesso do Termo em terras tupiniquins foi super legal também, teve até reações de ex-BBB pedindo ele em casamento por gostar tando do jogo. Parabéns Fer, acredito que você merece todo o sucesso e muito mais. Sou seu fã!
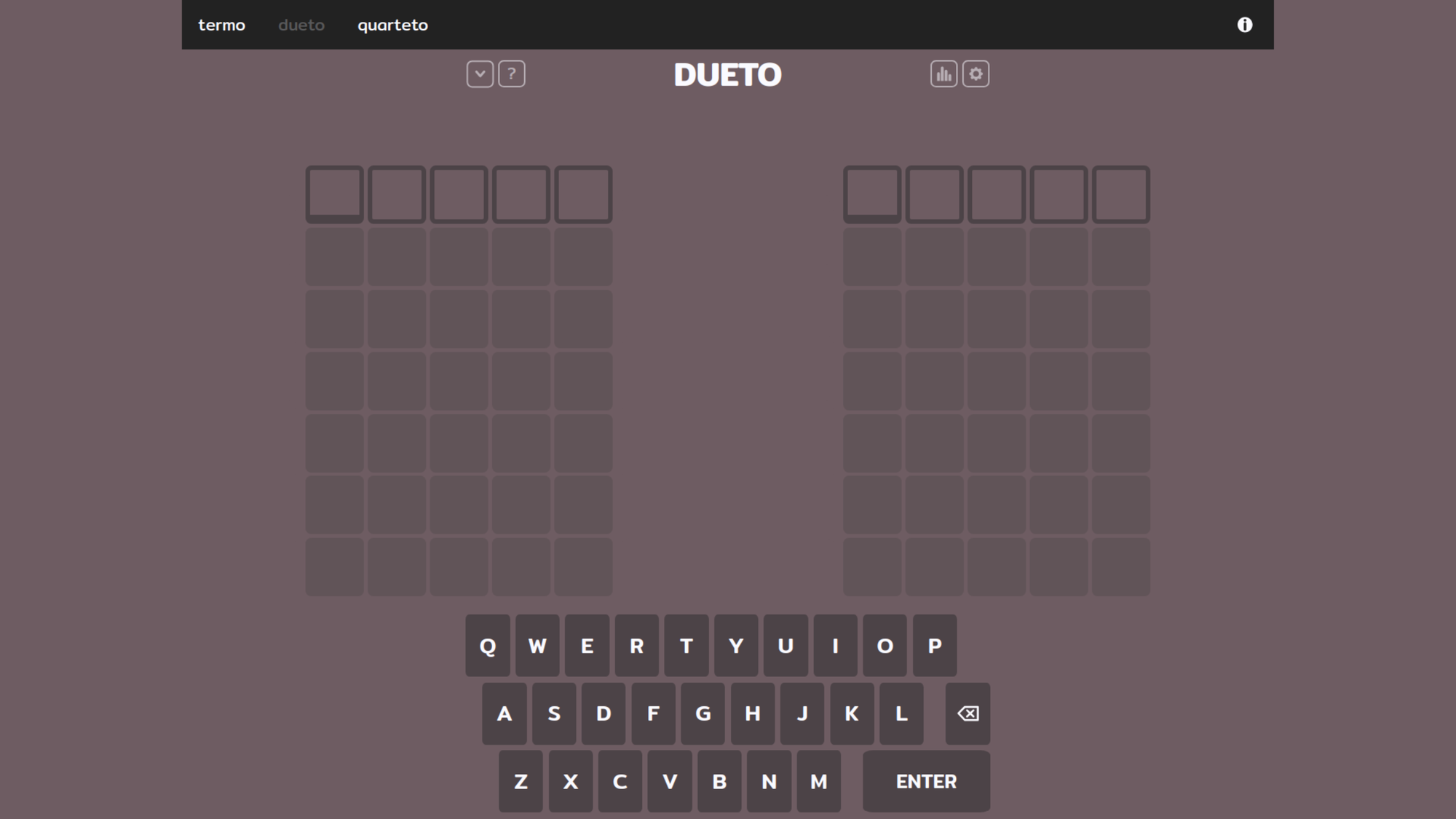
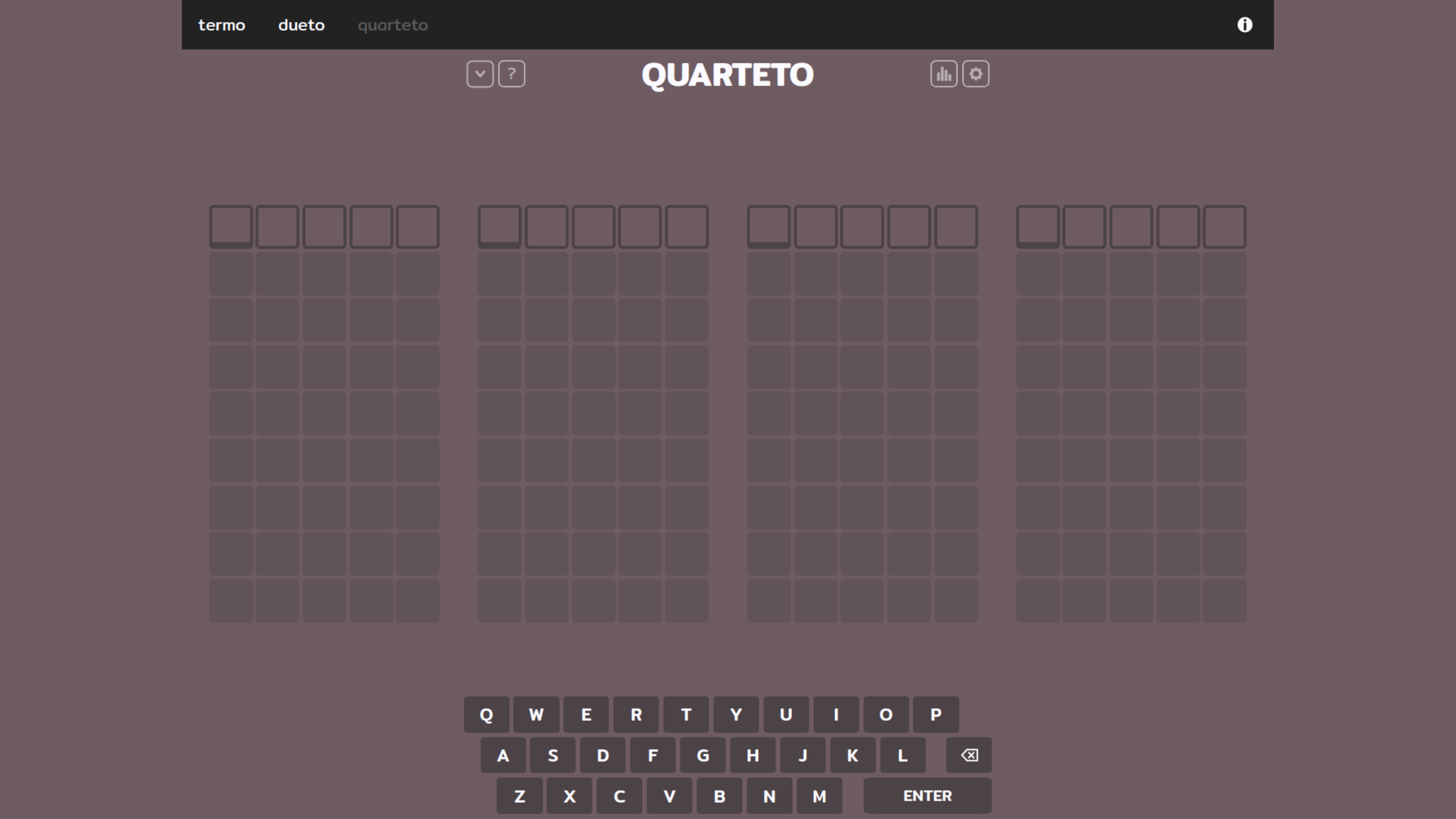
Já o Termo trás um modo de jogo ainda mais legal que tabuleiro convencional de seis tentativas. Com os desafios "dueto" e "quarteto" você pode deixar o desafio ainda mais interessante testando a mesma palavra em múltiplos tabuleiros ao mesmo tempo.
Assim como o casal do Wordle, minha esposa e eu desenvolvemos a mesma rotina de dedicar uns minutinhos para descobrir a palavra do dia. Criar o "nosso momento", a nossa fuga do mundo. Juntos e sem falar de trabalho, tínhamos a missão de colaborativamente resolver um problema.
Não é isso que é um relacionamento no final do dia? Uma dupla que se propõe a resolver os problemas da vida juntos?
E assim começa a nossa história: todos os dias às 9pm, independente de onde estivéssemos, fazíamos uma videoconferência e jogávamos juntos o Termo.
Otimizando o gameplay
Disclaimer
Para quem me conhece, já começou o texto estava esperando por essa sessão. "O Filipe não vai simplesmente querer jogar o joguinho...". Caso seja a primeira vez estejamos nos interagimos, me explico: eu gosto de mergulhar nas camadas mais profundas possíveis dos desafios que me são apresentados. É uma filosofia de vida. Abaixo vou descrever como o fiz.
No total, o Wordle documenta ter ~12.000 palavras de cinco letras do Inglês. Fernando conseguiu reunir ~10,500 palavras do Português para o Termo. É um volume zero assustador na realidade.
A partir de agora vou focar no somente no Termo, ok?
Aprendendo a jogar
O jogo consiste em tentar descobrir sets de ou 1, ou 2, ou 4 palavras de forma simultânea com um número máximo de tentativas que é linder à medida que o número de tabuleiros cresce. As tentativas crescem com a complexidade do jogo seguindo o comportamento:
\[ t = 5 + n \]
Onde t é o número de tentativas e n o número de palavras simultâneas.
Primeiro ponto de reflexão foi: mesmo que o número de tabuleiros e de possíveis tentativas cresçam, a dificuldade do jogo não parece aumentar. Suponho que a razão está em justamente que o número total de palavras, letras e combinações continuam constantes também enfrentando um número maior de tentativas. Veja, as tentativas acumulam eliminações de árvores de possibilidades para todos os tabuleiros ao mesmo tempo. Portanto, o jogo torna-se mais fácil quanto maior o número de tentativas, quanto maior o número de tabuleiros.
Agora... Se você gosta de estatística, aperte os cintos!
Quando me apresentou o jogo, meu irmão compartilhou ter uma estratégia inicial. Ele sempre começava o jogo com uma palavra que tivesse o máximo de vogais possível, pois dessa forma já eliminava uma grande árvore de possibilidades.
De fato fez todo sentido! No Inglês há consoantes que podem atuar como núcleo de uma sílaba sonorantes. Assim, é permitindo haver sílabas sem vogais explícitas, mas isso é algo que não ocorre na estrutura fonológica do Português. Nunca reparou? Olha aqui ["crypt", "glyph", "lynch", "myths", "nymph"].
Então, uma estratégia para iniciantes (eu, no caso) é claramente escolher uma "melhor palavra" e mensurar os resultados da tentativa t2 em diante.
Trazendo a Biba pra brincadeira
Depois de um tempo conversando, chegamos à obviedade que na língua portuguesa as vogais tem uma presença muito forte e, por isso, parece fazer sentido ir ainda mais além e sacrificar não somente a primeira tentativa, mas as duas primeiras para testar todas as vogais! Se você eliminar uma vogal, praticamente toda uma árvore enorme de possibilidade vai junto.
Chutamos duas palavras sem muito compromisso com alguma análise estatística. Começávamos todos os jogos com ["estar", "unido"], porque além de ser fofo, trazer todas as vogais, ainda tinha as consoantes ["s", "r", "n"] que são ótimos conectores ou finais de sílabas.
Ahh, curiosamente essa conclusão meu irmão já tinha chegado, inclusive já estava testando com ["reais", "mundo"].
Com essa abordagem decidi mudar as regras do jogo na minha cabeça. Na realidade o jogo passou a ser: tenho aqui uma lista de vogais e algumas consoantes, consegue descobrir qual palavra é com quatro tentativas?
Depois de alguns dias jogando me peguei que eu não gostava de usar a letra "d" como um dos testes principais. Parecia ser um palpite fraco para quebrar as árvores de combinações de palavras em Português. Mas é fraca de verdade mesmo?
O meu amadorismo começou a me irritar e o chamado pela melhor palavra ficou mais forte depois dessa dúvida. Para isso preciso de um banco de palavras para estudar.
Montando um dataset de palavras
Ao mesmo tempo, notei um detalhe em que o Termo se diferenciava do Wordle. Pelo Fernando se preocupar com a user experience (UX) do jogo, ele acabou por facilitar o jogo não intencionalmente. Simplificando o teclado para QWERT - sem caracteres especiais - o jogo precisa compensar a sua escolha de palavra com uma busca da palavra que mais aproxima dela. Se você digitar "arabe" o jogo corrige para "árabe". A versão em Inglês não precisa fazer isso para que o jogo tenha uma boa experiência, visto que não há acentos em Inglês.
Essa feature me ajudou a formular a primeira regra de negócio para o nosso dataset, chamei de sobreposição. A regra consiste em tirar todos os acentos e caracteres especiais - como acentos e o ce-cedilha "ç" - das palavras que levarmos para o nosso estudo. Eu trouxe o exemplo de "árabe", com uma sobreposição, mas olha "maçãs" e "macas, já com duas letras sobrepostas.
Por algumas madrugadas, explorei várias oportunidades e reuni o máximo de palavras do Português e Guarani que o tempo e paciência permitiram. Foram três principais fontes que se tornaram uma planilha única:
a) O Fernando gentilmente deixou disponível a lista que usou para fazer o jogo: https://github.com/fserb/pt-br
b) Fiz um pequeno crawler e conseguí vários artigos de sites de notícias.
c) Peguei uma lista de palavras de uma universidade brasileira, mas infelizmente esqueci qual.
| size | pt-br | Guarani | total |
|---|---|---|---|
| 5 | 10.497 (4% of all) |
92 (8,52% of all) |
10.589 |
| all | 261.798 | 1.079 | 262.877 |
Tabela 1: Tamanho final do dataset de palavras únicas após a remoção de réplicas e sobrepostas.
Filipe, mas por que Guarani? Por que existe um número não muito grande, porém muito usado no nosso dia-a-dia de palavaras do Guarani, como ["arara", "cutia", "canoa", "gambá", "mirim"]. Curiosamente as palavras são mais curtas que a média do Português, pelo que pude observar nos meus resultados.
Comecei por explodir as 10.589 palavras para comparar a frequência de cada letra em sua posição atual. O próximo passo foi gerar essa tabela secundária de frequência por posição:
| letter | p1 | p2 | p3 | p4 | p5 |
|---|---|---|---|---|---|
| a | 1152 | 2135 | 798 | 1985 | 2550 |
| o | 291 | 1598 | 428 | 765 | 2319 |
| e | 325 | 1515 | 542 | 1160 | 1183 |
| i | 250 | 1337 | 1007 | 1068 | 729 |
| r | 582 | 806 | 1172 | 699 | 712 |
| s | 700 | 126 | 555 | 295 | 1326 |
| u | 205 | 1177 | 561 | 402 | 461 |
| l | 487 | 354 | 725 | 328 | 376 |
| c | 1030 | 161 | 593 | 469 | 2 |
| m | 700 | 152 | 451 | 267 | 648 |
| t | 708 | 137 | 571 | 693 | 29 |
| n | 309 | 275 | 926 | 361 | 60 |
| p | 827 | 106 | 283 | 204 | 4 |
| d | 394 | 111 | 362 | 482 | 8 |
| b | 620 | 127 | 296 | 286 | 4 |
| g | 476 | 78 | 410 | 317 | 3 |
| f | 576 | 76 | 197 | 99 | 5 |
| v | 395 | 68 | 230 | 193 | 0 |
| h | 112 | 120 | 47 | 256 | 8 |
| z | 143 | 28 | 125 | 60 | 104 |
| j | 173 | 25 | 104 | 117 | 1 |
| x | 58 | 61 | 125 | 72 | 33 |
| q | 61 | 8 | 74 | 0 | 0 |
| k | 11 | 1 | 2 | 6 | 10 |
| y | 0 | 3 | 3 | 1 | 13 |
| w | 3 | 3 | 1 | 3 | 0 |
Tabela 2: Letras e suas frequências por posição.
Disclaimer: Sim, é por conta da junção desenfreada dessas bases que criei que surge um problema de qualidade dos dados. Como saber se aquela palavra existe ou se não é um typo? Essa palavra deveria estar mesmo no dataset? E já te adianto que ocorrem vários casos de siglas ["pcdob", "ibope", "paigc"]. WTF is paigc?
PAIGC (wikipedia)
O Partido Africano da Independência da Guiné e Cabo Verde, também conhecido pela sigla PAIGC, foi o movimento que organizou a luta pela independência da Guiné Portuguesa (Guiné-Bissau) e de Cabo Verde, que eram colónias de Portugal.
Apesar de ter gerado esse problema da qualidade dos dados, ainda considero que estamos no caminh correto. Tenho o objetivo de simular a solução vinda da cabeça humana que desconhece qual rol de palavras que o jogo usa.
Análises combinatórias
Vamos refletir um pouco sobre as possibilidades de análise scombinatórias que essa tabela nos trás. Dado que "a" é a letra mais frequente, qual a probabilidade de chutar qualquer palavra e conter ao menos um "a"? É relativamente mais fácil calcular a probabilidade do "a" não estar em cada uma das posições, e depois calculamos a porcentagem complementar.
\[ P(\text{não } A_1) = 1 - \frac{1.152}{10.589} \approx 1 - 0{,}1088 = 0{,}8912 \]
\[ P(\text{não } A_2) = 1 - \frac{2.135}{10.589} \approx 1 - 0{,}2017 = 0{,}7983 \]
\[ P(\text{não } A_3) = 1 - \frac{798}{10.589} \approx 1 - 0{,}0754 = 0{,}9246 \]
\[ P(\text{não } A_4) = 1 - \frac{1.985}{10.589} \approx 1 - 0{,}1875 = 0{,}8125 \]
\[ P(\text{não } A_5) = 1 - \frac{2.550}{10.589} \approx 1 - 0{,}2408 = 0{,}7592 \]
Assumindo que a ocorrência de "a" em cada posição é independente, a probabilidade de uma palavra não ter "a" em nenhuma posição é:
\[ P(\text{não } A_{\text{nenhuma}}) = P(\text{não } A_1) \times ...\times P(\text{não } A_5) \]
\[ P(\text{não } A_{\text{nenhuma}}) = 0{,}8912 \times 0{,}7983 \times 0{,}9246 \times 0{,}8125 \times 0{,}7592 \]
\[ P(\text{não } A_{\text{nenhuma}}) \approx 0{,}4065 \]
A probabilidade de uma palavra ter pelo menos um "a" é o complementar da probabilidade de não ter "a" em nenhuma posição:
\[ P(\text{pelo menos um } A) = 1 - P(\text{não } A_{\text{nenhuma}}) \]
\[ P(\text{pelo menos um } A) = 1 - 0{,}4065 = 0{,}5935 \]
\[ P(\text{pelo menos um } A) = 59{,}35\% \]
Tá, e daí? E daí que aprendi a calcular a probabilidade da presença de cada letra para um chute qualquer!
| # | letter | might not have | might have |
|---|---|---|---|
| 1 | a | 40.58% | 59.42% |
| 2 | o | 57.41% | 42.59% |
| 3 | e | 62.34% | 37.66% |
| 4 | i | 64.63% | 35.37% |
| 5 | r | 67.64% | 32.36% |
| 6 | s | 74.36% | 25.64% |
| 7 | u | 75.95% | 24.05% |
| 8 | l | 80.28% | 19.72% |
| 9 | c | 80.19% | 19.81% |
| 10 | m | 80.65% | 19.35% |
| 11 | t | 81.21% | 18.79% |
| 12 | n | 82.88% | 17.12% |
| 13 | p | 87.08% | 12.92% |
| 14 | d | 87.76% | 12.24% |
| 15 | b | 87.94% | 12.06% |
| 16 | g | 88.38% | 11.62% |
| 17 | f | 91.23% | 8.77% |
| 18 | v | 91.87% | 8.13% |
| 19 | h | 94.96% | 5.04% |
| 20 | z | 95.73% | 4.27% |
| 21 | j | 96.09% | 3.91% |
| 22 | x | 96.75% | 3.25% |
| 23 | q | 98.65% | 1.35% |
| 24 | k | 99.72% | 0.28% |
| 25 | y | 99.81% | 0.19% |
| 26 | w | 99.91% | 0.09% |
Tabela 3: Letras e suas probabilidades de estarem presentes nas palavras.
Agora consigo responder porque o "d" é um chute ruim, aparece em décimo quarto com 12,24% de probabilidade de estar presente na palavra.
Sabe o que é mais interessante? A probabilidade de termos ao menos uma das cinco vogais é de 97,75%. Daí imagino que 2,25% do dataset deva ser de palavras indesejadas ou não presentes no Português.
Também aprendi que a distribuição de vogais nas palavras fica com essas probabilidades [20.99%, 73.30%, 31.50%, 50.81%, 68.39%]. É muito provável que a segunda posição seja uma variável e que obviamente temos que ter uma vogal nas últimas duas posições.
Sabe outra coisa contra-intuitiva? Parece que verbos no infinitivo não parecem tão frequentes ou pelo menos está na mesma proporção de "ão".
Uma decepção que tive era a presença dos verbos no infinitivo. No Português os verbos nessa conjugação terminam em ["ar", "er", "ir"].
\[ P(p4 = a) = \frac{f_{p4}(a)}{N} = \frac{1.985}{10.589} \approx 0,1875 \text{ ou } 18,75\% \]
\[ P(p4 = e) = \frac{f_{p4}(e)}{N} = \frac{1.160}{10.589} \approx 0,1095 \text{ ou } 10,95\% \]
\[ P(p4 = i) = \frac{f_{p4}(i)}{N} = \frac{1.068}{10.589} \approx 0,1009 \text{ ou } 10,09\% \]
\[ P(p5 = r) = \frac{f_{p5}(r)}{N} = \frac{712}{10.589} \approx 0,06725 \text{ ou } 6,725\% \]
\[ P(\text{termina com "ar"}) = 0,1875 \times 0,06725 \approx 0,01262 \text{ ou } 1,262\% \]
\[ P(\text{termina com "er"}) = 0,1095 \times 0,06725 \approx 0,00736 \text{ ou } 0,736\% \]
\[ P(\text{termina com "ir"}) = 0,1009 \times 0,06725 \approx 0,00679 \text{ ou } 0,679\% \]
\[ P(\text{verbo}) = 0,01262 + 0,00736 + 0,00679 = 0,02677 \text{ ou } 2,677\% \]
Logo não basta chutar as vogais nas primeiras tentativas, você consegue ter um aumento de performance chutando as palavras que possuem a melhor distribuição das letras nas suas posições mais frequentes!
Em busca da melhor palavra
Em seguida, criei alguns atributos pra cada palavra para ajudar no ranking, trago alguns exemplos abaixo:
| word | richness | score_p1 | score_p2 | score_p3 | score_p4 | score_p5 | score |
|---|---|---|---|---|---|---|---|
| ibope | 5 | 250 | 127 | 428 | 204 | 1183 | 2192 |
| heroi | 5 | 112 | 1515 | 1172 | 765 | 729 | 4293 |
| cisco | 4 | 1030 | 1337 | 555 | 469 | 2319 | 5710 |
| curao | 5 | 1030 | 1177 | 1172 | 1985 | 2319 | 7683 |
Tabela 4: Tentativa de construção de um score baseado na soma das frequencias de cada letra na posição que se encontra.
a) richness: número total de letras não repetidas.
b) score_pX: frequência daquela letra naquela posição.
c) score: somatório das frequências.
O "score" aqui é basicamente brincar com os números sem nenhuma pretenção estatística. O objetivo é basicamente diferenciar uma letra da outra. Sendo assim, agora eu consigo fazer duplas de palavras e dizer se é uma boa combinação inicial ou não.
| w1 | w2 | richness | score_w1 | score_w2 | score |
|---|---|---|---|---|---|
| estar | unido | 10 | 3719 | 4288 | 8007 |
| turma | ileso | 10 | 5874 | 3760 | 9634 |
| reais | mundo | 10 | 5289 | 5604 | 10893 |
| clima | atrio | 10 | 5208 | 5848 | 11056 |
Tabela 5: Combinações de palavras para que o score somado seja poderoso!
Consegui chegar em uma combinação sensacional com as palavras certa (6960) e laico (6417) somando 13377, num richness de 9.
Surgem algumas discussões como por exemplo: é melhor abdicar um pouco de richness para ganhar em score e arriscar acertar as letras em suas posições? Cheguei à conclusão: não.
O jogo é uma sequencia acumulada de testes, e, por isso, sua missão é acumular o máximo de informação possível com o mínimo de tentativas. Assim você consegue esgotar todas as árvores possibilidades inválidas.
Chamei minha namorada para apresentar todo o meu aprendizado e minha planilha. Ela disse que é trapaça.
Agora, quando quero irritá-la, eu chuto quibe (3714) ou extra (4206). Apesar dela nunca ter visto essas tabelas, ela domina o Português e sabe muito bem das minhas reais intenções.
PS: Caso você pense parecido comigo e queira saber a pior palavra que consegui encontrar: ijebu (1564).
O pedido
Referências de pedidos
Leitor, se você nasceu na década de 80/90 é bem provavel que as suas referências devem ser muito parecidas com as minhas. Quando você pensa como deveria ser um pedido de casamento: ou você tem a história dos seus pais na cabeça ou de filmes de comédia romântica da época.






E não são poucos...!
| Nome do Filme | Enredo | Pedido de Casamento |
|---|---|---|
| Pretty Woman (Uma Linda Mulher; 1990) | Um empresário frio se apaixona por uma acompanhante contratada para acompanhá-lo em eventos sociais. | Edward (Richard Gere) faz o pedido subindo em uma limusine com flores até a janela de Vivian (Julia Roberts). Ele supera o medo de compromissos sérios. Vivian chora de felicidade. Sem anel. |
| Father of the Bride (O Pai da Noiva; 1991) | Um pai superprotetor tenta lidar com a ideia de sua filha se casar com o homem que ela ama. | Bryan (George Newbern) faz o pedido a Annie (Kimberly Williams) durante um jantar em família, oferecendo um anel simples e tocante. |
| Four Weddings and a Funeral (Quatro Casamentos e um Funeral; 1994) | Uma comédia romântica sobre os altos e baixos do amor através de casamentos e funerais. | Charles (Hugh Grant) faz o pedido a Carrie (Andie MacDowell) sob a chuva, depois de quase se casar com outra pessoa. Eles superam as dúvidas sobre o amor. Ambos emocionados. |
| Jerry Maguire (Jerry Maguire – A Grande Virada; 1996) | Um agente esportivo tenta reconstruir sua carreira enquanto descobre o verdadeiro amor. | Jerry (Tom Cruise) faz um pedido apaixonado e impulsivo a Dorothy (Renée Zellweger) em casa, dizendo: "Você me completa." Sem anel, mas muitas lágrimas. |
| The Wedding Singer (Afinado no Amor; 1998) | Um cantor de casamentos e uma garçonete apaixonam-se enquanto ambos estão comprometidos com outras pessoas. | Robbie (Adam Sandler) faz o pedido no avião, cantando uma música personalizada para Julia (Drew Barrymore). Ele supera seu medo de fracassar no amor. O ambiente tem passageiros emocionados. Não há anel. Julia chora de alegria. |
| Runaway Bride (Noiva em Fuga; 1999) | Uma mulher famosa por fugir de casamentos começa a questionar seus próprios medos quando se apaixona por um jornalista. | Ike (Richard Gere) faz o pedido em um momento íntimo na casa dele, com Maggie (Julia Roberts) finalmente enfrentando seu medo de compromissos. Há um anel simples. Ambos emocionados. |
| Notting Hill (Um Lugar Chamado Notting Hill; 1999) | Um dono de livraria e uma estrela de cinema tentam navegar as diferenças de seus mundos enquanto se apaixonam. | Anna (Julia Roberts) faz o "pedido" em uma livraria, pedindo que William (Hugh Grant) a aceite como ela é. O conflito envolve a insegurança de William sobre a diferença de status entre eles. Não há anel, mas há sinceridade e emoção. William aceita com um sorriso. |
| A Walk to Remember (Um Amor Para Recordar; 2002) | Um bad boy se apaixona por uma jovem devota que ensina a ele lições de amor e fé antes de perder a batalha contra uma doença terminal. | Landon (Shane West) faz o pedido na varanda da casa de Jamie (Mandy Moore), com um anel de família. O conflito é a aceitação da doença terminal de Jamie. Ambos emocionados. |
| Sweet Home Alabama (Doce Lar; 2002) | Uma designer de moda de sucesso deve enfrentar seu passado ao voltar para sua cidade natal para se divorciar do marido. | Jake (Josh Lucas) faz o pedido na praia, com um anel escondido dentro de um pedaço de vidro de trovão. O momento é íntimo e emocionante. |
| 50 First Dates (Como Se Fosse a Primeira Vez; 2004) | Um homem se apaixona por uma mulher com perda de memória recente e precisa reconquistá-la todos os dias. | Henry (Adam Sandler) não faz um pedido tradicional. Ele cria um vídeo que resume o amor deles e propõe viverem juntos no barco. O conflito é a perda de memória de Lucy (Drew Barrymore). Há emoção e lágrimas. |
| The Proposal (A Proposta; 2009) | Uma chefe fria propõe casamento a seu assistente para evitar ser deportada, e eles acabam descobrindo sentimentos reais. | Andrew (Ryan Reynolds) faz o pedido no escritório em frente aos colegas de trabalho. Ele supera a mágoa inicial pela farsa de Margaret (Sandra Bullock). Não há anel, mas há um discurso emocionante. Margaret chora. |
| Leap Year (Casa Comigo?; 2010) | Uma mulher viaja para a Irlanda para propor casamento a seu namorado no dia 29 de fevereiro, mas acaba se apaixonando por outra pessoa no processo. | Declan (Matthew Goode) faz o pedido a Anna (Amy Adams) na Irlanda, no topo de um penhasco, após superar o medo de abrir seu coração novamente. Sem anel, mas com emoção sincera. |
| The Time Traveler’s Wife (Te Amarei Para Sempre; 2009) | Um homem com uma condição genética que o faz viajar no tempo luta para manter seu casamento com a mulher que ama. | Henry (Eric Bana) faz o pedido de casamento a Clare (Rachel McAdams) no meio de uma conversa casual em casa. Ele não tem um anel, mas promete um futuro juntos. Há emoção. |
| About Time (Questão de Tempo; 2013) | Um jovem descobre que pode viajar no tempo e usa essa habilidade para viver um amor extraordinário. | Tim (Domhnall Gleeson) faz o pedido de casamento a Mary (Rachel McAdams) em casa, de pijama, enquanto assistem TV. Ele supera a ansiedade sobre o momento perfeito. Sem anel. |
Quando eu revejo essa lista buscando por inspirações, hnmm... Nheh. Todos os pedidos são muito feitos para funcionar na tela do cinema, a maioria fica longe da realidade humana que o dia-a-dia traz. Há até alguns insights legais como o vídeo do Adam Sandler em 50 First Dates com os melhores momentos da vida do casal.
Mas, sinceralmente? Decidi que o melhor é perguntar pra ela.
Para a minha surpresa, minha namorada foi direto ao ponto: "Pra mim o pedido tem que ser simples, íntimo, só nosso, com a nossa cara. Sem ninguém em volta. Ambos sendo nós mesmos."
Não sei você leitor, mas eu escolhi bem demais.
Conectando os pontos
Leitor, acredito que depois da jornada que te fiz passar, deixei claro que este momento recorrente era importante para nós. Não só porque somos pessoas que gostamos de desafios! Mas nos unia de forma inocente para resolver um problema, mesmo que apartados. Meu pedido tinha que ser sobre esse momento.
Brainstorm
Preciso fazer com que o jogo se comporte diferente do esperado.
a) Fazer um proxy estilo man-in-the-middle para que quando ela acessasse
Retrições:
1. Só funcionaria dentro
Comments ()